(Paper Review) Multi-Layer Perceptron (MLP)
Paper Link : https://www.cs.toronto.edu/~graves/preprint.pdf
Multi layer Perceptron
가장 널리 사용되는 Feed-forward Neural Network 형태가 MLP이다.
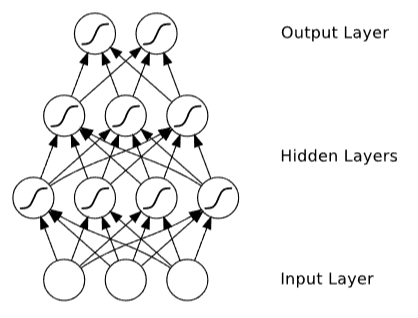
MLP는 상호 연결된 단위 계층으로 구성되며 입력 패턴은 입력 계층에 표시되고 숨겨진 계층을 통해 출력 계층으로 전파된다. 이 프로세스를 네트워크의 Forward Pass 라고 한다.
MLP의 출력은 현재 입력에만 의존하고 과거 또는 미래의 입력에는 의존하지 않으므로 Sequence Labeling 보다 패턴 분류에 더 적합하다. 특정 가중치 값 세트를 가진 MLP는 입력 벡터에서 출력 벡터로의 함수를 정의한다. 가중치를 변경하여 단일 MLP가 다양한 함수를 인스턴스화 할 수 있다.
그림의 MLP의 은닉 레이어와 출력 레이어의 S자형 곡선은 S자형 non-linear activate funtion 적용을 나타낸다. 이러한 함수는 네트워크에 비선형성을 도입하여 입력과 출력 간의 복잡한 관계를 모델링할 수 있도록 한다.
Forward Pass
MLP의 첫 번째 은닉 계층의 각 단위는 입력 단위의 가중치 합계를 계산한다.이 합계를 단위 h에 대한 네트워크 입력값이라고 하며 ah로 표시된다.그런 다음 활성화 함수 θh를 ah에 적용하여 bh로 표시된 단위가 최종 활성화된다.단위 i에서 단위 j까지의 무게는 wij로 표시된다.

위 식은 은닉 유닛 h에 대해 네트워크 입력값 ah를 계산하는 방법을 보여준다. 이 값은 가중치 wij와 입력값 xi의 곱을 곱한 값입니다. 여기서 i 범위는 1부터 I까지. 이 방정식은 hidden unit에 대한 가중치 입력의 합계이다.
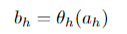
위 식은 hidden unit h에 대한 최종 활성화 bh가 어떻게 계산되는지 보여준다. 이는 활성화 함수 θh를 네트워크 입력값 ah에 적용한 결과다.이 식은 hidden unit의 활성화가 해당 단위의 네트워크 입력에 활성화 함수를 적용한 결과이다.
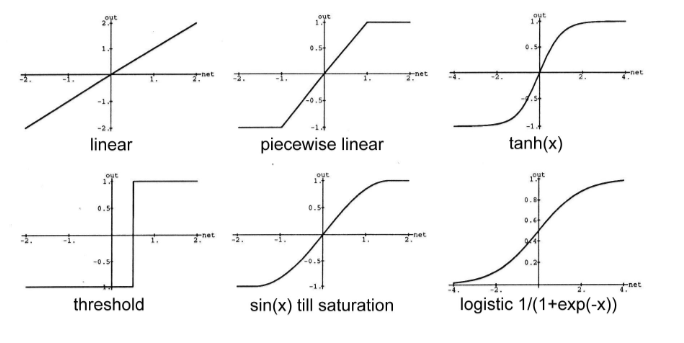
MLP에서 일반적으로 loss function 로 Tanh(), sigmoid() 를 사용한다.
두 함수 모두 비선형인데, 이는 비선형 신경망이 선형 신경망보다 강력하기 때문.
두 함수의 또 다른 중요한 특성은 미분이 가능하다는 것인데, 이를 통해 네트워크를 경사하강법으로 훈련시킬 수 있다.
1. 표현 능력: 비선형 활성화 함수를 사용하는 비선형 신경망은 더 다양한 함수 형태를 표현할 수 있다. 반면에 선형 활성화 함수만을 사용하는 선형 신경망은 입력과 가중치의 선형 조합으로 표현되는 한계가 있다. 비선형 활성화 함수를 통해 신경망은 비선형 함수, 곡선 등 다양한 형태의 함수를 모델링할 수 있어 더 복잡한 관계를 표현할 수 있습니다.
2. 패턴 학습 능력: 비선형 신경망은 복잡한 데이터의 패턴을 학습하는 능력이 뛰어나다. . 이는 신경망이 고차원의 비선형 패턴을 인식하고, 예측 및 분류 작업에 더 뛰어난 성능을 발휘할 수 있게 합니다. 선형 신경망은 입력 데이터의 선형 관계만을 학습할 수 있으므로, 비선형 문제에는 제한적인 성능을 보인다. 따라서, 비선형 신경망은 선형 신경망보다 더 많은 종류의 함수를 표현하고, 더 복잡한 패턴을 학습하는 능력을 가지므로, 비선형 문제에 더 강력하게 대응할 수 있다.
즉, activation 함수는 넓은 범위의 입력값을 받아 더 작은 범위의 출력값에 매핑한다.
첫 번째 hidden layer 에 있는 유닛의 activation function를 계산한 후 나머지 hidden layer에 대해 이 프로세스가 반복된다.
Backward Pass
gradient descent 및 backpropagation를 사용하여 신경망을 훈련시키는 과정. MLP는 미분 가능한 연산자이므로 gradient descent을 사용하여 미분 가능한 손실 함수를 최소화하도록 훈련할 수 있다.gradient descent는 각 네트워크 가중치에 대한 손실 함수의 도함수를 찾고 음의 기울기 방향으로 가중치를 조정하는 데 사용되는 방법이다.
backpropagation는 편도함수에 대한 chain rule을 반복적으로 적용하는 것이다.
역전파의 첫 번째 단계는 출력 단위를 기준으로 손실 함수의 도함수를 계산하는 것이다. 그 다음 chain rule을 사용하여 숨겨진 단위에 대한 손실 함수의 도함수를 계산한다. 이러한 방식으로 chain rule을 반복적으로 적용하면 네트워크의 모든 가중치에 대한 손실 함수의 도함수를 효율적으로 계산할 수 있다.